万年暦というものがありますが、累計日数を計算すれば簡単に作れます。次のような簡単な関数で、ほぼキリスト誕生からの日数になります。
#define leap(y) ((y)%4 == 0 && ((y)%100 != 0 || (y)%400 == 0))
static int DaysOfMonth[2][12] = {
31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31,
31, 29, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31 };
static int md[2][12] = {
0, 31, 59, 90, 120, 151, 181, 212, 243, 273, 304, 334,
0, 31, 60, 91, 121, 152, 182, 213, 244, 274, 305, 335 };
int TotalDays(int y, int m, int d)
{
int ty = y - 1;
int t = ty * 365 + ty / 4 - ty / 100 + ty / 400;
t += md[leap(y)][m - 1];
return t + d;
}
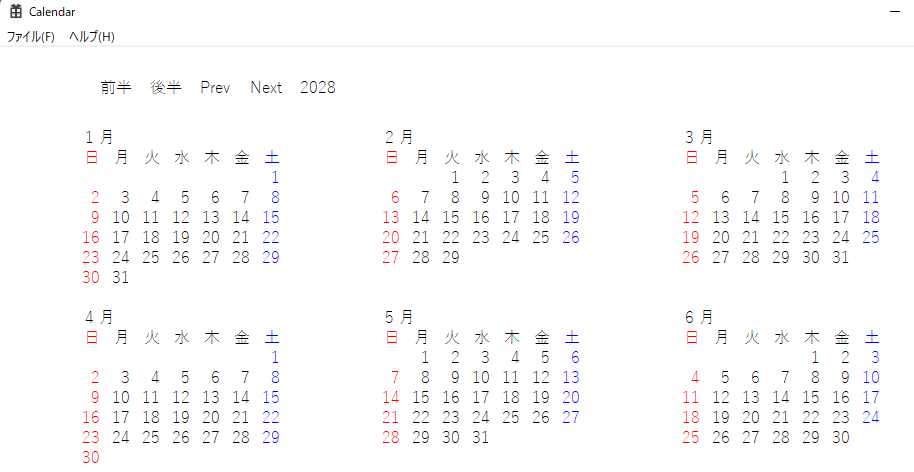
プログラムを動かすと次のようになります。

操作としては前半をクリックすると1月から6月まで、後半をクリックすると7月から12月までの表示になります。PrevとNextをクリックすると前の年や次の年になります。次の例は三年後のカレンダーです。
年の表示をクリックすると入力できます。
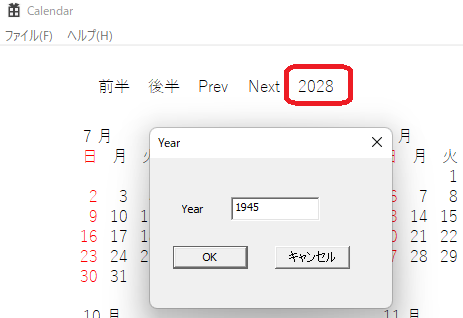
次のものは1945年のカレンダーです。

次のような関数を使えば累計日数から日付に戻せます。つまり、ある日から1000日後というような日付を求めることができます。例を示そうかと思いましたが、手間がかかるのでやめました。
int ipM[366 * 2];
BOOL bIpm;
void TotalToDate(int td, int& y, int& m, int& d)
{
// year
td--;
int ya = td / (365 * 400 + 97);
int t1 = td % (365 * 400 + 97);
int yb = t1 / (365 * 100 + 24);
int t2 = t1 % (365 * 100 + 24);
int yc = t2 / (365 * 4 + 1);
int t3 = t2 % (365 * 4 + 1);
int yd = t3 / 365;
int t4 = t3 % 365;
if (t1 == 365 * 400 + 96) // leap year : 400
{
y = (ya + 1) * 400;
t4 = 365;
}
else
{
if (yd > 3) // leap year : 4
{
yd = 3;
t4 = 365;
}
y = ya * 400 + yb * 100 + yc * 4 + yd + 1;
}
// month
// static int *ipM = NULL; // work : not yet deleted ?????????????
if (!bIpm)//ipM)
{
// ipM = new int[366 * 2];
int at = 0;
for (int i = 0; i < 12; i++)
{
int n = DaysOfMonth[0][i];
for (int j = 0; j < n; j++)
{
ipM[at++] = i + 1;
}
}
for (int i = 0; i < 12; i++)
{
int n = DaysOfMonth[1][i];
for (int j = 0; j < n; j++)
{
ipM[at++] = i + 1;
}
}
}
int yy = leap(y);
m = ipM[yy * 365 + t4];
// day
d = t4 - md[yy][m - 1] + 1;
}
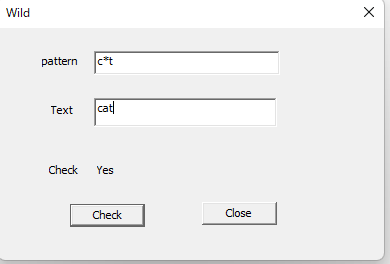
ワイルドカードというものがあり、*は任意の文字列 ?は任意の一文字にマッチします。たとえばc*tにはcatやcourtがマッチします。形式言語学で言うと、ワイルドカードは正規表現の一種なのでオートマトンの応用で判定できます。たとえばc*tとcatを考えます。
c * t -> c * t -> c * t -> c * t
^ c ^ a ^ ^ t ^ ^ ^
まずスタート位置にコマ(^)を置きます。文字が一致すれば次に進みます。パターンが?の時にはどの文字にもマッチします。パターンが*の時には、元の位置にも残して次の位置にもコマを進めます。このようにして、最後にゴール地点にコマがあればマッチしたことになります。
以前に考えたコードに間違いがあったようで、複数のコマがある情況では処理が衝突することがあるので、いったん新しい所に作成して書き戻すようにしました。またc*tにctをマッチさせるにはイプシロン遷移という処理が必要です。とりあえず、動いています。
BOOL IsWild()
{
int lenP = lstrlen(pat);
int lenS = lstrlen(str);
for (int i = 0; i < 100; i++)
bWild[i] = FALSE;
bWild[0] = TRUE;
for (int i = 0; i < lenS; i++)
{
for (int j = 0; j <= lenP; j++)
bNext[j] = FALSE;
int c = str[i];
for (int j = 0; j < lenP; j++)
{
int d = pat[j];
if (bWild[j])
{
switch (d)
{
case '*':
bNext[j] = TRUE;
bNext[j + 1] = TRUE;
break;
case '?':
bNext[j + 1] = TRUE;
break;
default:
if (c == d)
bNext[j + 1] = TRUE;
break;
}
}
}
for (int j = 0; j <= lenP; j++)
bWild[j] = bNext[j];
for (int j = lenP; j > 0; j--)
{
if (bWild[j - 1] && pat[j - 1] == '*')
bWild[j] = TRUE;
}
}
return bWild[lenP];
}